[Fortran] 查看源码 复制源码
module fft
use MKL_DFTI
implicit none
real(8), parameter :: pi = dacos(-1.0D0)
contains
subroutine fft1d(n, x_in, x_out)
implicit none
integer, intent(in) :: n
complex(8), intent(in) :: x_in(n)
complex(8), intent(out) :: x_out(n)
type(DFTI_DESCRIPTOR), pointer :: My_Desc_Handle
Integer :: Status
Status = DftiCreateDescriptor( My_Desc_Handle, DFTI_DOUBLE, DFTI_COMPLEX, 1, n )
Status = DftiSetValue( My_Desc_Handle, DFTI_PLACEMENT, DFTI_NOT_INPLACE)
Status = DftiCommitDescriptor( My_Desc_Handle )
Status = DftiComputeForward( My_Desc_Handle, x_in, x_out )
Status = DftiFreeDescriptor(My_Desc_Handle)
end subroutine
subroutine ifft1d(n, x_in, x_out)
implicit none
integer, intent(in) :: n
complex(8), intent(in) :: x_in(n)
complex(8), intent(out) :: x_out(n)
type(DFTI_DESCRIPTOR), pointer :: My_Desc_Handle
Integer :: Status
Status = DftiCreateDescriptor( My_Desc_Handle, DFTI_DOUBLE,DFTI_COMPLEX, 1, n )
Status = DftiSetValue( My_Desc_Handle, DFTI_PLACEMENT, DFTI_NOT_INPLACE)
Status = DftiSetValue( My_Desc_Handle, DFTI_BACKWARD_SCALE, 1.0D0/N)
Status = DftiCommitDescriptor( My_Desc_Handle )
Status = DftiComputeBackward( My_Desc_Handle, x_in, x_out )
Status = DftiFreeDescriptor(My_Desc_Handle)
end subroutine
subroutine fft_1st_deriv_1d(N, x_in, deriv_x, L)
implicit none
integer, intent(in) :: N
complex(8), intent(in) :: x_in(N)
complex(8), intent(out) :: deriv_x(N)
real(8), intent(in) :: L
complex(8) :: fft_x(N), dfft_x(N)
integer :: k
real(8) :: kx(N)
call fft1d(N, x_in, fft_x)
do k = 1, N
if(mod(N,2) .eq. 0) then
write(*,*) N
if( k .eq. N/2+1) then
kx(k) = 2*pi/L*0
dfft_x(k) = cmplx(0.0D0, 1.0D0,kind=8)*kx(k)*fft_x(k)
else if(k .le. N/2) then
kx(k) = 2*pi/L*(k-1)
dfft_x(k) = cmplx(0.0D0, 1.0D0,kind=8)*kx(k)*fft_x(k)
else
kx(k) = 2*pi/L*(k-1-N)
dfft_x(k) = cmplx(0.0D0, 1.0D0,kind=8)*kx(k)*fft_x(k)
end if
else
if(k .le. N/2) then
dfft_x(k) = 2*pi*dcmplx(0.0D0, 1.0D0)/L*(k-1)*fft_x(k)
else
dfft_x(k) = 2*pi*dcmplx(0.0D0, 1.0D0)/L*(k-N-1)*fft_x(k)
end if
end if
end do
call ifft1d(N, dfft_x, deriv_x)
open(unit = 16, file="dfft.txt")
end subroutine
end module fft
program test
use fft
implicit none
integer, parameter :: n =128
complex(8) :: x_out(n), z(n), deriv_x(n), x_in(n)
! real(8), parameter :: pi = 4.0D0*datan(1.0D0)
real(8) :: l =2*pi
integer(8) :: i
real(8) :: dt
write(*,*) pi
do i = 1, n
! x_in(i) = exp(dcmplx(0.0D0,2.0D0*pi)*real(i)/n)
x_in(i) = cmplx(cos(2*pi*(i-1)/(n-1)),kind = 8)
end do
call fft1d(n,x_in,x_out)
call ifft1d(n,x_out,z)
call fft_1st_deriv_1d(n,x_in, deriv_x, l)
end program test
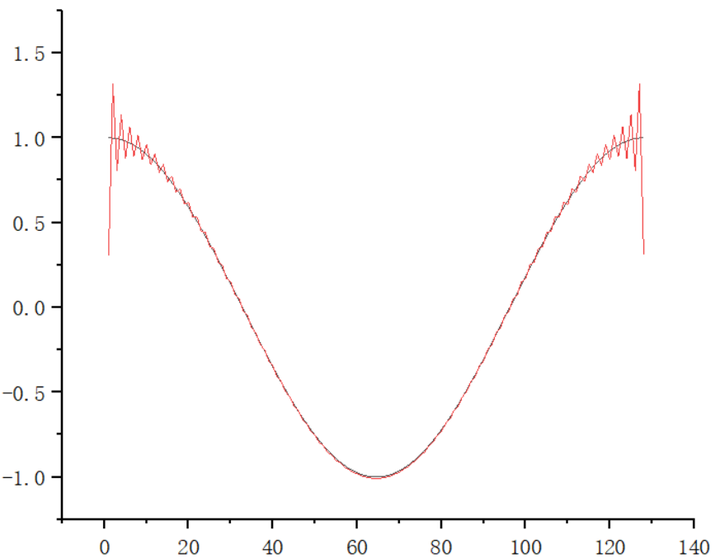 )
) )
)